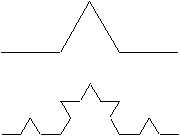
Az alábbi példában a görbe felbontását rekurzív módon végtelenül finomítva egy ún. Koch görbét kapunk. Ez már egy önhasonló, fraktális objektum.

Rajzoljunk fraktálokat!
Tartalomjegyzék:
A fraktálok két tulajdonságát szokták kiemelni.
- Önhasonló objektumok
Az egyes részeit kinagyítva az eredetihez többé kevésbé hasonló objektumot
kapunk.
- Törtdimenziójú objektumok
Definiálhatunk egy fraktális dimenziót a következőképpen. Osszuk fel az
objektumot N darab egybevágó, az eredetihez hasonló részre. A hasonlóság
aránya legyen r. Így a fraktális dimenzió: D = log N / log (1
/ r).
Nézzünk néhány példát ezen definíció alkalmazására:
A képet geometriai transzformációk sorozatos ismétlésével (ún. iterált függvényrendszerek segítségével) állíthatjuk elő.
Az affin transzformációk kicsinyítést, eltolást és forgatást tartalmazhatnak.
Lényeges, hogy kontraktívak legyenek, azaz tetszőleges ponthalmazt transzformálva
csökkenjen a pontok közötti távolság.
A véletlenszerű választás az egyes transzformációk közül úgy történjen,
hogy azokra, amelyek az eredeti kép nagyobb hányadát lefedő részhez tartoznak
arányosan gyakrabban kerüljön sor.
Példák:
1. A négyzetet négy részre osztottuk fel, amelyekhez az alábbi transzformációkat rendelhetjük:
 |
1. x' = x / 2 | y' = y / 2 | ||
| 2. x' = x / 2 + a / 2 | y' = y / 2 | |||
| 3. x' = x / 2 | y' = y / 2 + a / 2 | |||
| 4. x' = x / 2 + a / 2 | y' = y / 2 + a / 2 |
Pascal nyelven a fraktáltenisz algoritmusa
2. A már bemutatott Koch görbét szintén négy, az eredetihez hasonló résszel fedhetjük le:
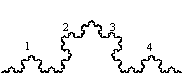 |
1. kicsinyítés 1/3-ára | |||||||
| 2. kicsinyítés 1/3-ára | forgatás 60°-kal | eltolás "a"-val | ||||||
| 3. kicsinyítés 1/3-ára | horizontális tükrözés | forgatás 120°-kal | eltolás "2a"-val | |||||
| 4. kicsinyítés 1/3-ára | eltolás "2a"-val |
Pascal nyelven a fraktáltenisz algoritmusa
3. A klasszikus példa, egy természetes objektum, páfrány kirajzolása:
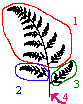 |
1. kicsinyítés | forgatás | eltolás függőlegesen | |||
| 2. kicsinyítés | forgatás | eltolás függőlegesen | ||||
| 3. kicsinyítés | forgatás | eltolás függőlegesen | ||||
| 4. x' = x / 500 | y' = y / 4 |
Pascal nyelven a fraktáltenisz algoritmusa
Feladatok:
Készítsük el az alábbi alakzatokat kirajzoló fraktáltenisz algoritmusokat!
 |
 |
 |
 |
Az eddig látott fraktális alakzatok önhasonló tulajdonsága miatt szinte kínálja magát a rekurzív előállítási módszer. Természetesen így csak egy közelítést kapunk, a rekurzív hívásoknak valamikor le kell állniuk, de ez praktikusan egybeeshet a képernyő felbontásával.
Példák:
1. A már jól ismert Koch görbe:
Pascal nyelven a rekurzív algoritmus
2.
Pascal nyelven a rekurzív algoritmus
Feladatok:
Készítsük el az alábbi alakzatokat kirajzoló rekurzív algoritmusokat!
 |
 |
Vizsgálódjunk a komplex számsík közepe táján. Egy komplex szám a következő
alakban írható fel: z = x+ yi , ahol x-t és
y-t a szám koordinátájaként képzelhetjük el, x a valós y
a képzetes rész.
Induljunk ki egy számból (pl. z = 0 + 0i), majd végezzük
el rajta sorozatosan egymás után a következő műveletet: z := z2
+ c , ahol c = a + bi egy állandó komplex szám.
Ekkor z bolyongani kezd a komplex számsíkon, kaotikus viselkedést mutat.
Elképzelhető, hogy z a végtelenbe menekül, azaz a nagysága (távolsága
a számsíkon az origótól) a végtelenhez tart. Mandelbrot - halmaznak nevezzük
azon c komplex számok halmazát, amelyre z nagysága bármely
számú művelet elvégzése után is véges marad. (A halmazt Benoit B. Mandelbrot
amerikai tudósról nevezték el.). Ha z-t nem 0-ról indítjuk, akkor a halmaz
egy torzított változatát kapjuk.
A halmaz szélén az egyes részeket újra és újra kinagyítva visszatérő, egymáshoz
hasonló motívumokat, indákat, spirálokat fedezhetünk fel. Nem véletlenül
nevezte Hubbard a Mandelbrot - halmazt a matematika legbonyolultabb képződményének.
Mandelbrot - halmaz előállítása
Bár a halmaz maga végtelenül bonyolult, mégis egy viszonylag egyszerű
algoritmussal kirajzolhatjuk. Vegyük sorra a komplex számokat a számsík
egy területén. Ezek lesznek c értékei. Minden c esetén z nulla értékéből
kiindulva végezzük a z := z2
+ c iterációt. Figyeljük, hogy z nagysága milyen gyorsan tart végtelenhez
(hány iteráció után éri el pl. a 100-at), és az egyes iteráció számokhoz
egy-egy színt rendelünk. Ha bizonyos számú iteráció (pl. 100) után sem
értük el a küszöbértéket, akkor ezt a c számot a Mandelbrot - halmazhoz
tartozónak könyvelhetjük el.
Ezek után egy kérdés maradt, hogy a komplex számsík mely területéről induljunk
ki. Ha a (-2 ; -1,25), (0,5 ; 1.25) téglalapon pásztázzuk végig a c értékét,
akkor az egész halmazt megkapjuk. Ezen területen kívül a z a végtelenhez
tart.
Szebbnél szebb alakzatokat kaphatunk, ha a halmaz szélein az egyes területeket
ismételten kinagyítjuk.
Egy lehetséges megvalósítása a teljes Mandelbrot - halmazt kirajzoló algoritmusnak.
Az alábbi képen a teljes Mandelbrot - halmazt láthatjuk. Rákkattintva végigkövethetünk egy nagyítássorozatot.
A Mandelbrot - halmaz rajzolásakor a z := z2
+ c képletben a c értéke tartozik a komplex számsík egyes pontjaihoz.
Maga a Mandelbrot - halmaz is végtelenül bonyolult, de ráadásul még minden
pontjához, azaz minden c értékhez tartozik egy Julia - halmaz, amelyet
úgy kapunk, hogy az adott c értéknél a z kezdő értékét pásztázzuk
a komplex számsík egy területén, és vizsgáljuk az iteráció során a z
végtelenbe menekülését. A halmazok Gaston Julia francia matematikusról
kapták a nevüket.
A Julia - halmazok rajzolása során megfigyelhetjük, hogy ha a c
pontot a Mandelbrot - halmaz belsejéből választjuk, akkor a halmaz összefüggő,
ha a Mandelbrot - halmazon kívülről választjuk, akkor pedig több darabból
áll.
Egy lehetséges megvalósítása a Julia- halmazt kirajzoló algoritmusnak.
Az alábbi képecskére kattintva egy kis kirándulást tehetünk a Julia - halmazok világában
1. A. K. Dewney: A számítógép mint mikroszkóp behatolhat a matematika
legbonyolultabb területeire, Tudomány 1985/2. 8-13. o.
2. A. K. Dewney: Szépség és mélység: a Mandelbrot-halmaz, valamint Julia
nevű rokonainak serege, Tudomány 1988/1. 6-10. o.
3. A. K. Dewney: Hogyan változtassuk a képzelet csapongását fraktálflórává
és -faunává?, Tudomány 1990.